コラム

検出力分析について

検出力分析あるいは検定力分析とは、統計的に有意であると判断するp値の基準（有意水準α）と、期待される効果の大きさ（効果量）およびサンプルサイズから、真に効果が存在した場合にその効果を正しく検出できる確率（検出力β）を見積もる試みです。検出力は通常0.8（80％）程度に設定され、この検出力を満たすようにサンプルサイズを増減させることで、実験や調査に必要なサンプルサイズを算出していく、というのが一般的な使われ方となっています。
検出力分析を行うことで、注目したい効果が現実的な意味をもつような大きさをもっているのかを考慮しながら、統計的仮説検定を行うことができます。もちろん、微小な効果の検出が学術的な意味を持つこともありますが、広く世間で用いられる統計的仮説検定の目的を考えると、「果たしてその効果が現実的な意味をもつのか」という視点は重要であると言えるでしょう。ある施策をうつことによる売り上げへの効果が微小であるなら、例えそれが数千人という単位の調査の結果統計的に有意であったとしても、施策自体のコストが売り上げへの効果を上回ってしまう、という本末転倒なことにもつながってしまうかもしれません。

相関係数について

一口に相関係数と言っても様々な種類がありますが、今回は最も一般的に用いられているピアソンの積率相関係数を前提として話をしていきたいと思います。
相関係数はある2変数間の線形的な関連性の強さを表したものであり、－1から＋1までの値の範囲をとります。相関係数が－1もしくは＋1の場合、片側の変数の変動によってもう片側の変数の変動が線形的に完全に説明されるような状態を示しています。具体例をあげると、等速直線運動を行う物体の進む距離と経過時間は完全に線形的な関係性を持っています。当たり前ですが、秒速1メートルで進む物体であれば5秒経てば5メートル進んでいますし、秒速2メートルなら5秒で10メートル進んでいます。こうした、片側の変数の値がわかればもう片側の変数の値も確定するような（線形的に）完全な関係性の場合、相関係数は－1もしくは＋1になります。
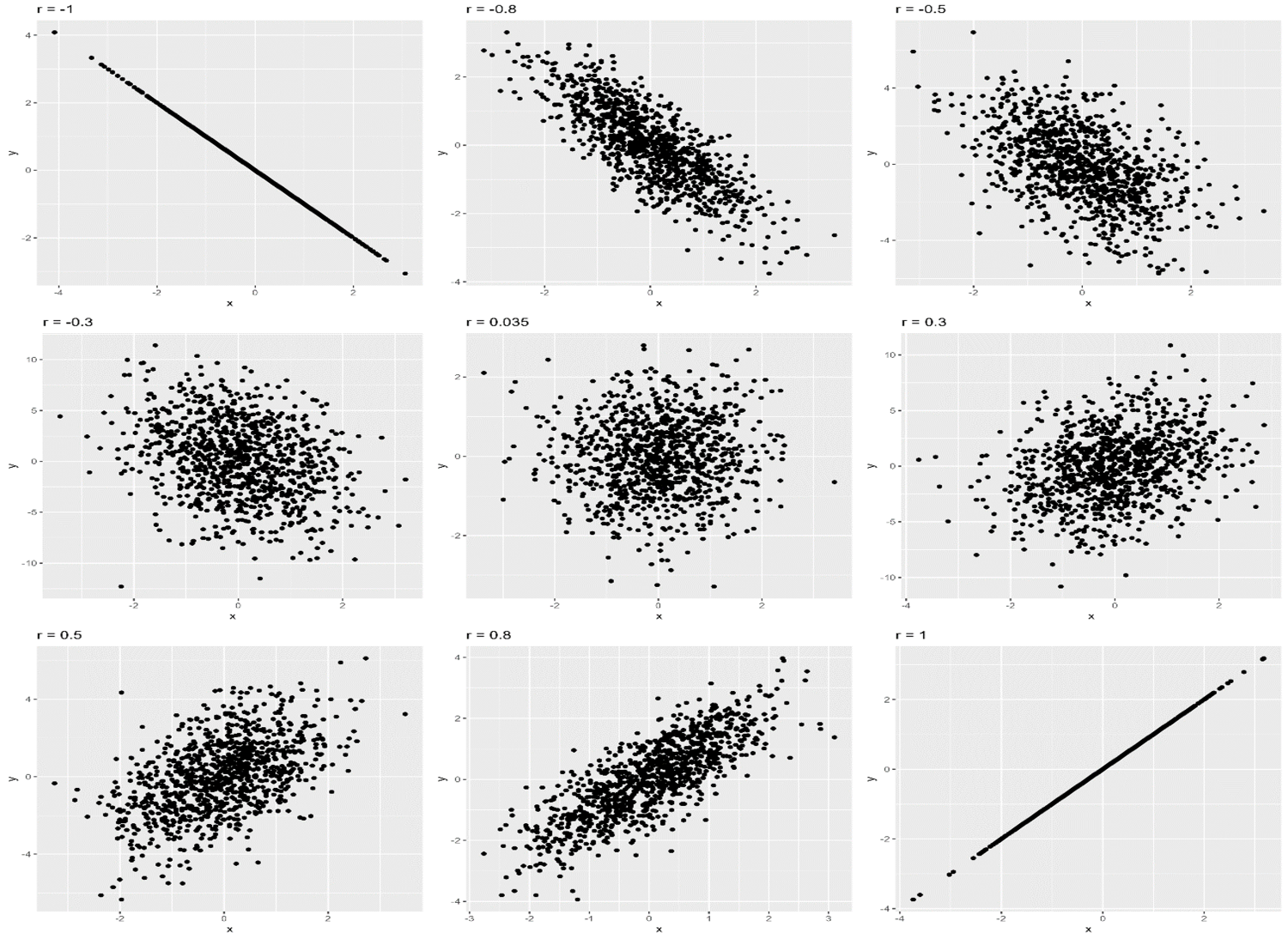
しかしながら、我々が注目するような変数のほとんどは上記のような完全な関係性を持っていないため、相関係数が完全に－1や＋1になることは現実のデータではほぼ存在しないでしょう。2変数間の相関関係の強さはしばしば散布図（Scatter Plot）と呼ばれる図で可視化され、片側の変数を固定したときのもう片側の変数の値のばらつきが大きいほど、相関係数の絶対値は小さいことになります（下図参照）。

検出力分析における相関係数の制約

さて、ようやく本題となりますが、当然相関係数についての統計的仮説検定を行う場合にも検出力分析を実施してサンプルサイズを見積もることが推奨されています。相関係数は効果量の一種であるため、検出力分析に使用する効果の大きさは仮定される相関係数の値を入力することになります。この時、先行研究や事前調査などにより相関係数の値が定まっているのであればよいのですが、多くの場合未知の関連性についての検証であるため、この効果の大きさは研究者や調査者の経験的知見などに依拠することになります。この場合に、想定される相関係数には理論的な上限が存在する、というのがTilburg & Tilburg (2023)による指摘です。
例えば、1つの例として決定係数（R2）を用いた上限値の確認を取り上げていきたいと思います。決定係数は分散説明率や寄与率などとも呼ばれ、ある変数X1の変動が、別の変数X2やX3などの変動によってどの程度説明できるかを表した値です。この値は（今回の話の文脈では母集団における真の決定係数を前提としているため）0から1までの値の範囲をとります。実務上では決定係数が1を超えたり、あるいは0を下回る現象も目にしますが、ここではあくまで理論的な前提の話であるので注意してください。
そのため、もしも事前に仮定した相関構造において、この決定係数が1を超えるようなことがあれば、それは理論的にありえない構造を仮定していることになります。3つの変数（X1,X2,X3）間の相関関係を考える場合、X1についての決定係数は

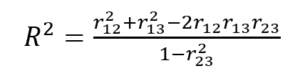
と表されます。ここで、例えばX1とX2、X1とX3に強い正の相関である0.7の相関係数、X2とX3の間に非常に強い負の相関である-0.9の相関を仮定した場合、理論的な決定係数が1.764／0.36で約4.9となってしまい、上限であるはずの１を大きく超えます。このように、「X1とX2、X1とX3が正の相関を示す一方、X2とX3は負の相関を示す」ような関係性は理論的な矛盾を抱えてしまいやすいです。しかし、例えば「製品の売り上げはTVのCM頻度と正の相関をもつ」「同じく、製品の売り上げはYoutube広告の頻度と正の相関をもつ」「しかし、広告宣伝費の兼ね合いからTVのCM頻度とYoutube広告の頻度は負の相関をもつ（片側が多ければ、片側は少ない）」というような構造を考えた場合、上記のような理論的にありえない効果量の設定を行ってしまうことはありそうです。

まとめ

今回は、近年推奨され、そして広まってきた効果量に基づく検出力分析およびサンプルサイズの設計について、普段注目されづらい部分に触れた論文を取り上げて紹介させていただきました。細かい話となってしまったので、あまり興味のない方にはつまらない話であったかもしれませんが、サンプルサイズ設計などの話を聞いたときに少しでも思い出していただけましたら幸いです。

センタンでは、脳波や心拍、皮膚電気活動などの生体情報の計測・解析から、ヒトの状態や影響などを深く知るサポートを行っています。研究・開発支援（受託研究）や生体データの利活用支援など様々な課題解決のサポート実績がございますので、興味を持たれた方がいらっしゃいましたら、どうぞお気軽にお問合せください。

引用文献

van Tilburg, W. A. P., & van Tilburg, L. J. A. (2023). Impossible hypotheses and effect-size limits. Advances in Methods and Practices in Psychological Science, 6(4), Article 25152459231197605.
https://doi.org/10.1177/25152459231197605

● 引用・転載について

• 当コンテンツの著作権は、株式会社センタンに帰属します。
• 引用・転載の可否は内容によりますので、こちらまで、引用・転載範囲、用途・目的、掲載メディアをご連絡ください。追って担当者よりご連絡いたします。

● 免責事項

• 当コンテンツは、正確な情報を提供するよう努めておりますが、掲載された情報の正確性・有用性・完全性その他に対して保証するものではありません。万一、コンテンツのご利用により何らかの損害が発生した場合であっても、当社およびその関連会社は一切の責任を負いかねます。
• 当社は、予告なしに、コンテンツやURLの変更または削除することがあり、また、本サイトの運営を中断または中止することがあります。